College Druidique des Gaules

Remarquons d'abord qu'un système minéral tend vers une position d'équilibre stable en suivant pour cela une évolution régie par le principe de moindre action (l'énergie y est minérale). Dans la forme vivante s'ajoute un principe de croissance avec la loi d'économie de la substance. Nous allons donc constater des harmonies basées sur 3 et 4 dans les systèmes cristallins, alors que les êtres vivants développeront une harmonie basée sur le nombre 5. Les exemples d'un cristal de neige et d'une ammonite nous montrent la différence entre les deux systèmes.

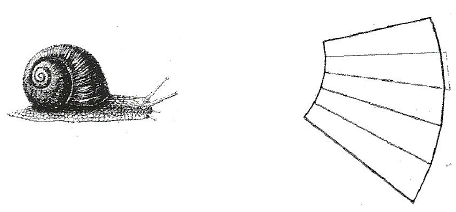
Nous allons examiner plusieurs cas de formes vivantes. Un, l'escargot qui construit une coquille de forme constante pour y loger son corps en croissance selon les trois dimensions (classe des non vertébrés). deux, le tournesol qui dispose ses feuilles aux mieux pour réaliser la photosynthèse. Trois, la pomme de pin qui organise ses bractées selon deux spirales croisées.

L'escargot. Si l'on ajoute des quantités dans la même proportion sur les quatre côtés d'un quadrilatère, ce dernier conserve ses angles internes. L'escargot utilise cette propriété géométrique qui lui permet de conserver intacte la forme de sa coquille, tout en l'agrandissant dans un rythme spiralé. Que ce soit un Petit gris ou un escargot de Bourgogne, la continuité est assurée par le procédé, et non par la forme initiale de sa coquille. Pour réussir ce tour de force il utilise seulement le principe de la série de Fibonacci.

Le tournesol. Pour que la photosynthèse soit maximale, il ne faut pas que les feuilles se superposent, sinon elles masqueraient le soleil à leurs voisines. Le tournesol y arrive en faisant pivoter progressivement ses feuilles autour de la tige selon le rythme de 8 feuilles en 3 tours complets. La solution mathématique est bien sur le partage du cercle selon le Nombre d'or. Mais la plante n'ayant pas fait de hautes études, elles se contente d'appliquer la série naturelle de Fibonacci.

La pomme de pin. Elle dispose ses bractées selon des spirales se croisant perpendiculairement et dont les nombres peuvent varier de 2 sur 2 jusqu'à 8 sur 13. Il s'agit encore de la série de Fibonacci. L'inégalité des nombres permet le recouvrement des bractées qui peuvent ainsi protéger efficacement les organes reproducteurs de la plante.

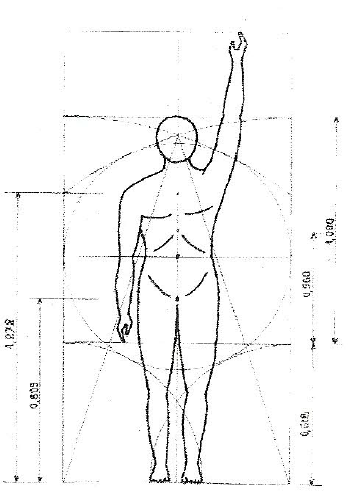
N'oublions pas les dimensions du corps humain. L'exemple le plus connu est le rapport déterminé par la position du nombril au centre du corps. Mais les phalanges de la main forment également une série 1, Ø, Ø2.

Et pour ma part j'ajouterai le persil. Il se développe selon le rythme  1 sur 2. A chaque nœud il part une tige principale et deux tiges secondaires. Nous sommes, avec cet exemple, encore avec la série de Fibonacci. Bien sûr, l'exemple du bouton de tournesol est beaucoup plus spectaculaire. On peut compter 89 spirales dans un sens et 144 dans le sens perpendiculaire. Un tournesol géant a même donné les nombres 144 et 233. Mais ce serait oublier que tous les végétaux cités ci-dessus partent d'un même point de départ, la série de Fibonacci.

Druide /I\ Kevrinel