Qu'est-ce que le Nombre d'or
Avant de se focaliser sur sa valeur arithmétique comme nous le faisons à notre époque, le Nombre d'or fut essentiellement pratiqué en utilisant des méthodes graphiques. Facilement reproductible à l'aide du compas et de l'équerre, sa construction se révèle très précise. c'est la raison pour laquelle il est resté très longtemps dans le seul domaine de la géométrie. Autrefois les moyens de calcul étaient plus limités qu'aujourd'hui.
Le Nombre d'or est un nombre réel, il ne peut donc pas être représenté par une fraction. Il est défini ainsi : Ø = [(1 + √5) / 2] = 1,618033988. Par la suite, nous emploierons la valeur usuelle, bien plus simple, Ø = 1,618, avec une erreur de seulement 2/100.000 (cette précision dépasse de très loin ce que nous savons réaliser dans le domaine pratique).
Le symbole utilisé pour désigner ce nombre est la lettre grecque phi (Ø), en souvenir de Phidias, sculpteur et architecte athénien qui a participé à la construction du Parthénon pendant le Siècle de Périclès.
On peut définir le nombre ainsi:
1) Le Nombre d'or représente le "partage en moyenne et extrême raisons" des Eléments d'Euclide.
2) Il partage à profusion les figures à base cinq, tels que les pentagones et décagones, qu'ils soient étoilés ou non. Notez que l'études de ces figures était à la base de l'enseignement pythagoricien.
3) Enfin, depuis Pacioli, il est la racine de l'équation du second degré : X2 - X - 1 = 0.
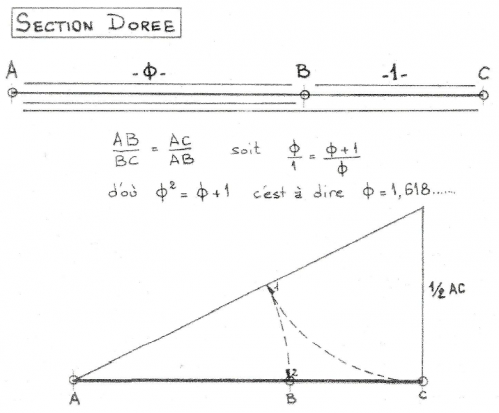
pour le dessiner, nous partons de la définition de Vitruve. Il nous dit qu'il y a 'Sectio aurea' (la section dorée en latin), c'est à dire un partage selon le Nombre d'or, "s'il y a de la petite partie à la grande le même rapport que la grande au tout". La figure suivante nous donne la méthode pour construire cette 'Section dorée' (ainsi que la 'Divine proportion' de Pacioli).
Si la longueur du segment BC de la figure ci-dessous vaut un, alors la longueur du grand segment AB vaut 1,618. Nous avons ainsi réalisé une proportion dorée, Ø = 1,618.Voici donc une première figure importante en relation avec le Nombre d'or.
Maintenant nous allons étudier une deuxième figure.
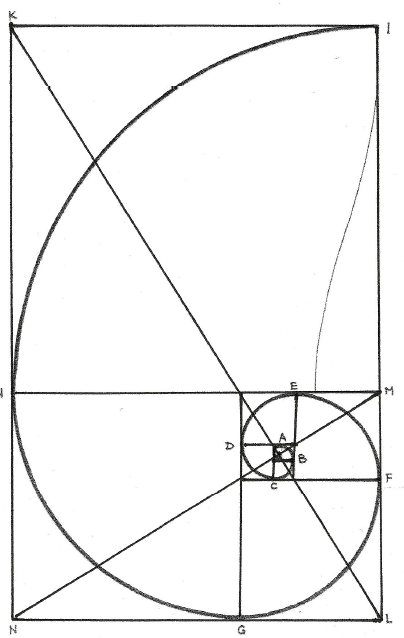
Pour ce faire, il nous faut d'abord dessiner une série de rectangles d'or.
Qu'est-ce qu'un rectangle d'or? C'est tout simplement un rectangle dont les deux côtés principaux sont dans le rapport Ø = 1,618. La particularité de ce rectangle est que, lorsqu'on lui ajoute un carré dont le côté est égal au grand côté du rectangle d'or, le nouveau rectangle ainsi constitué est lui aussi un rectangle d'or. On dit que le carré est le gnomon du rectangle d'or.
Sur la figure suivante, le rectangle ABCD est un rectangle d'or. En ajoutant le carré ADE nous obtenons un nouveau rectangle BCDE qui selon la définition précédente est un rectangle d'or. En ajoutant le carré BEFM, le rectangle CDEF est encore doré. Et ainsi de suite pour les rectangles DEFG, EFGH, FGHI, etc. On pourrait théoriquement continuer à l'infini si la taille du papier le permettait. Hélas, la taille du papier est limitée et par là même la série.
Traçons un quart de cercle CD de centre le sommet du carré lui faisant face. Prolongeons le par un autre quart de cercle DE dessiné dans le carré suivant. Continuons avec les quarts de cercle EF, FG, GH, HI, etc. Nous obtenons une figure géométrique spiralée.
Il se pose alors une question; Est-ce que la spirale converge vers un point précis? La réponses est positive. En traçant les deux diagonales KL et MN qui gèrent toute l'organisation des rectangles d'or de la série, j'obtiens un point de croisement qui est l'asymptote de la spirale.
Nous avons ainsi le dessin complet de la spirale dorée qui est une autre figure importante en relation avec le Nombre d'or.
Druide /I\ Kevrinel
A découvrir aussi
- La magie des plantes - les fruits et légumes
- Les influences de la Lune sur les plantes
- Les recettes de l'Ovate
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 42 autres membres